MetaMoJi ClassRoom先生　授業例

【高2 数学】領域と最大・最小（線形計画法）

大分県　大分県立臼杵高等学校　菅淳司先生

■ 単元目標

・軌跡について理解し，簡単な場合について軌跡を求めること。
・簡単な場合について，不等式の表す領域を求めたり領域を不等式で表したりすること。
・座標平面上の図形について構成要素間の関係に着目し，それを方程式を用いて表現し，図形の性質や位置関係について考察すること。
・数量と図形との関係などに着目し，日常の事象や社会の事象などを数学的に捉え，iPadなどの情報機器(GeogebraやMetaMoJi)を用いて軌跡や不等式の表す領域を座標平面上に表す等して，問題解決に活用したり，解決の過程を振り返って事象の数学的な特徴や他の事象との関係を考察したりすること。

■ MetaMoJi ClassRoom を導入した利点と成果

・線形計画法の問題は従来の板書を中心とした学習では、図形的な考察ができにくく、生徒は具体的にイメージできないことが多かった。また、図形の思考と、式の意味の考察の両面が必要であるため、生徒にとっては分かりにくく難解な問題であった。
・MetaMoJiを利用したことにより、図形の平行移動がスムーズに行え、考察が容易になった。
・グループ学習ページを設定したことにより、１つの図形を複数人で操作・考察してさまざまな意見を出し合ったことにより、思考の幅が広がった。

■ 学習活動

1.提示問題

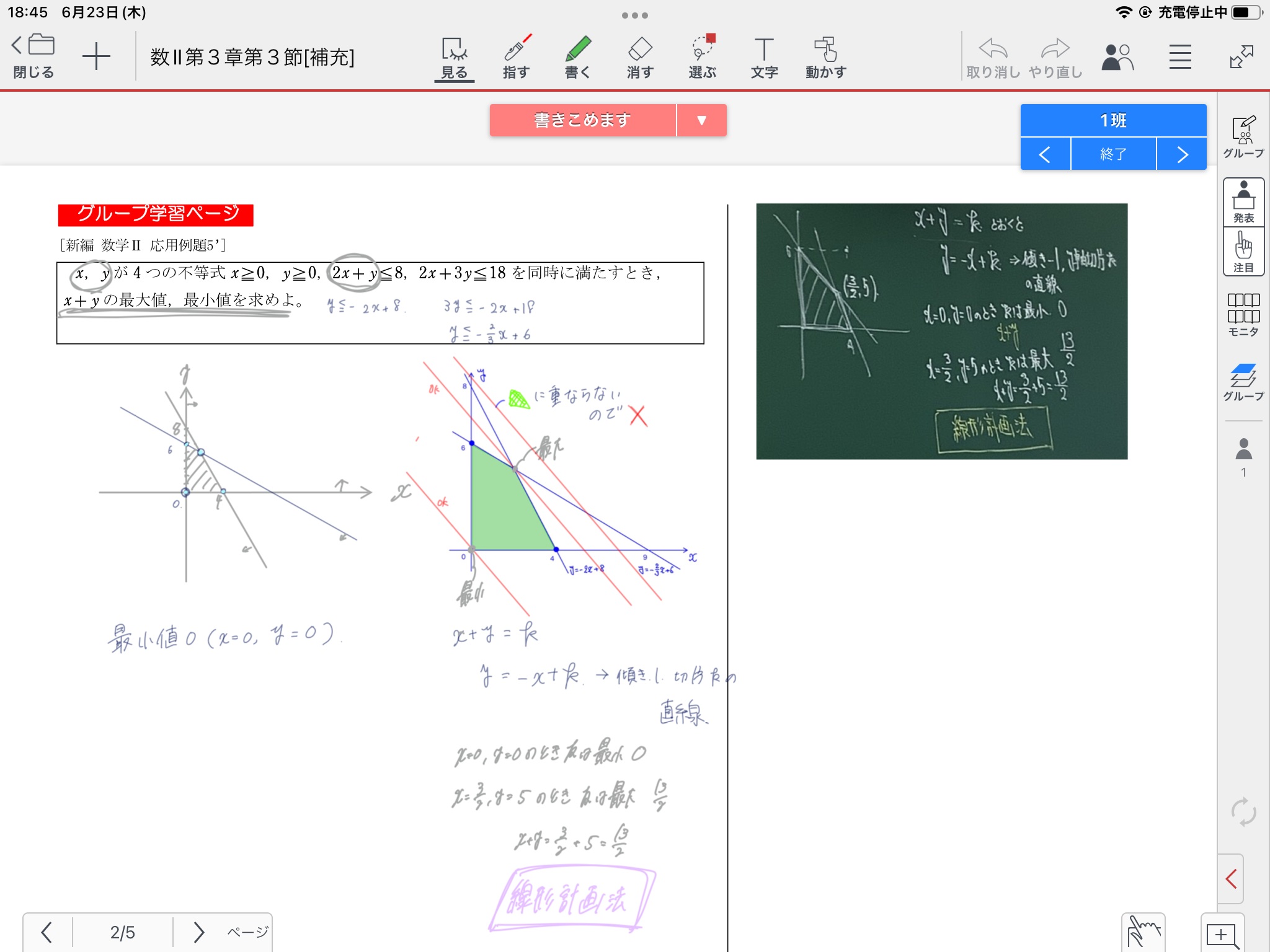
　x,yが2つの不等式x≧0、y≧0、2x+y≦0、2x+3y≦18を同時に満たすとき、x+yの最大値・最小値を求めよ。

同じ問題を１ページ目「個別学習ページ」、２ページ目「グループ学習ページ」に設定して配布。最初の数分はまず自分で考え(思考錯誤して)、その後グループ学習としたが、個人の思考の過程を残せるように配慮した。

2.生徒の活動

特にグループ活動に移行した場面では、領域を協力して描き、x+yの意味を考えていた。
その後、「x+y=kとおく」というヒントのみを与えたが、そのヒントを元に、自分たちの描いたグラフで直線を平行移動したりして考察を行っていた。
グループ内で考えを共有して、考察を深めていた。

3.提示問題２

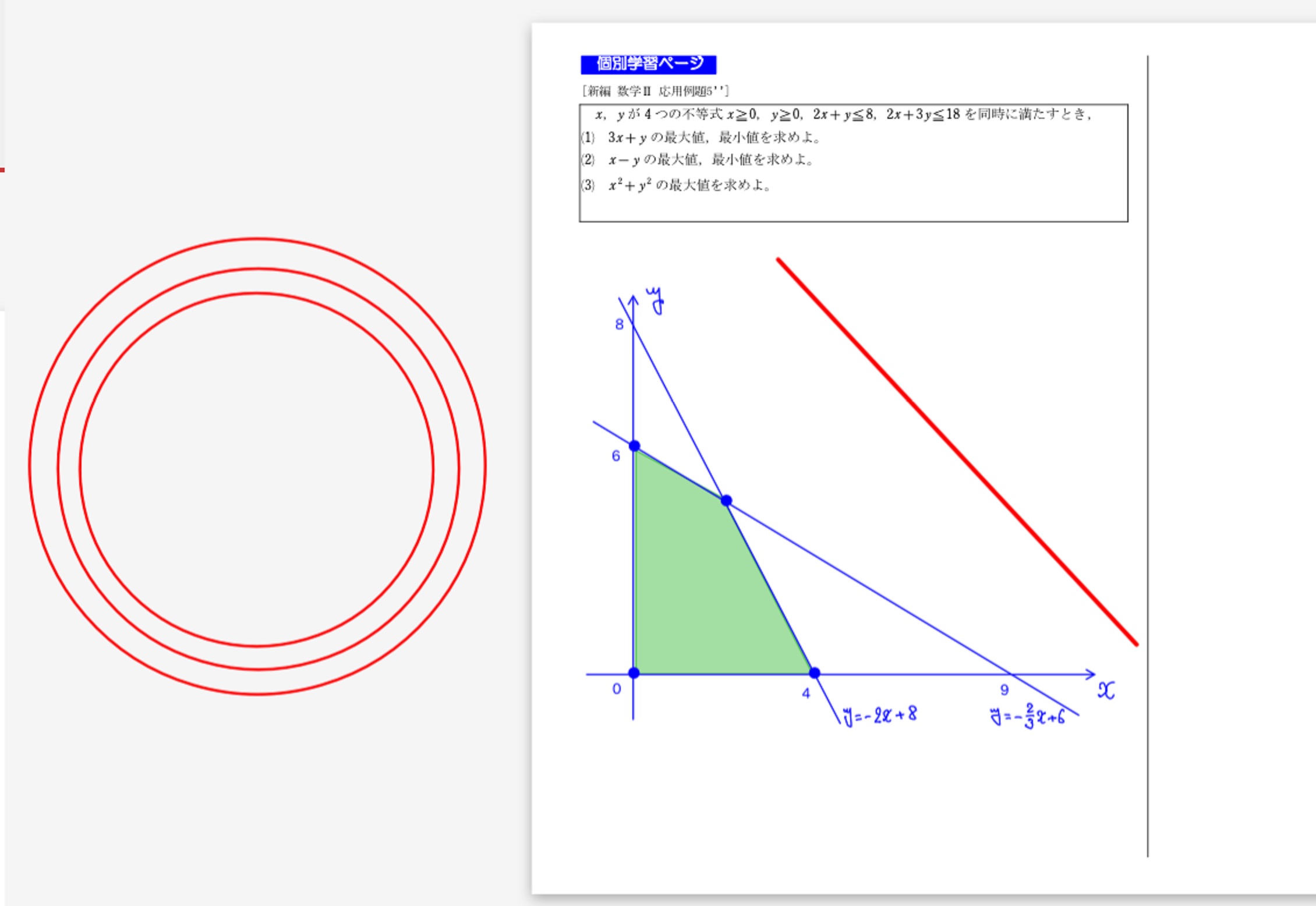
x,yが2つの不等式x≧0、y≧0、2x+y≦0、2x+3y≦18を同時に満たすとき、x+yの最大値・最小値を求めよ。
(1)　3x+yの最大値・最小値を求めよ。
(2)　x-yの最大値最小値を求めよ。
(3)　x^2+y^2の最大値を求めよ。

追加３問について、図形的な意味を考察し、MetaMoJiの図形を利用しながらグループ内で考察した。
・既に図形的なイメージができていたので、考察がスムーズになっていた。
・領域は同じものであることを告げると、前に描いたグラフをコピペして利用する姿も見られた。