MetaMoJi ClassRoom先生 授業例
【中3 数学】正方形の辺の長さとその大小関係 (啓林館 2章 平方根)
熊本県 熊本市立植木北中学校 堀之内聖二先生
■ 単元目標
- 面積がaである複数の正方形を作図し、その1辺の長さを、無理数も含めて数直線上で比較することができる。
- 無理数の存在を認識し、その表現方法を知る。
- 無理数も含めて、簡単な数の大小関係を不等号を使って表す。
■ MetaMoJi ClassRoom を導入した利点と成果
メタモジの図形機能を使い、いろいろな面積の正方形を作らせ、数直線上に並べることで、無理数の存在を確認するとともに大小関係をつかませた。
- iPadを利用することで生徒の興味関心を高めることができた。クイズ感覚で楽しみながら取り組んでいた。
- 自らが作成した正方形を、自ら数直線上でならべることで、無理数が数直線上に存在する数字であることが実感できていた。また、受動的ではなく、自発的に作業に取り組めた感を与えることができた。
- 作業の進み具合をリアルタイムで確認できるので、作業が遅れている生徒の取りこぼしが生まれなかった。
- 他のアプリでは残らないが、配布したワークシート内で取り組むので、復習にいつでも活用できる。
■ 学習活動
1.方眼の中に、4,9,36の面積の正方形を作る
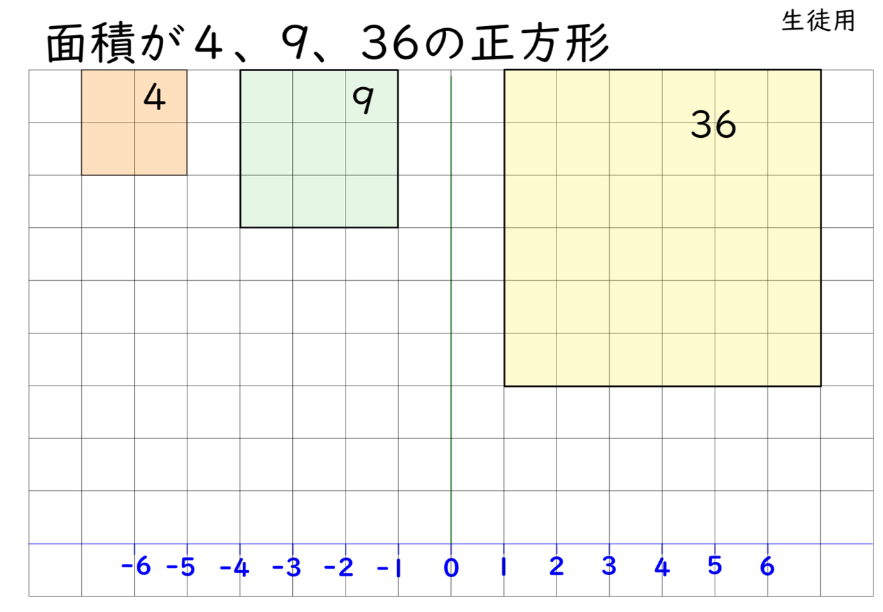
(画像クリックで拡大)
- 作った正方形の左端を、座標軸の原点に移動させて、1辺の長さを確認する(2,3,4)
- 作った正方形の右端を、座標軸の原点に移動させて、1辺の長さを利用して負の数を確認する(-2,-3,-4)
2.方眼の中に、2,5,8の面積の正方形を作る
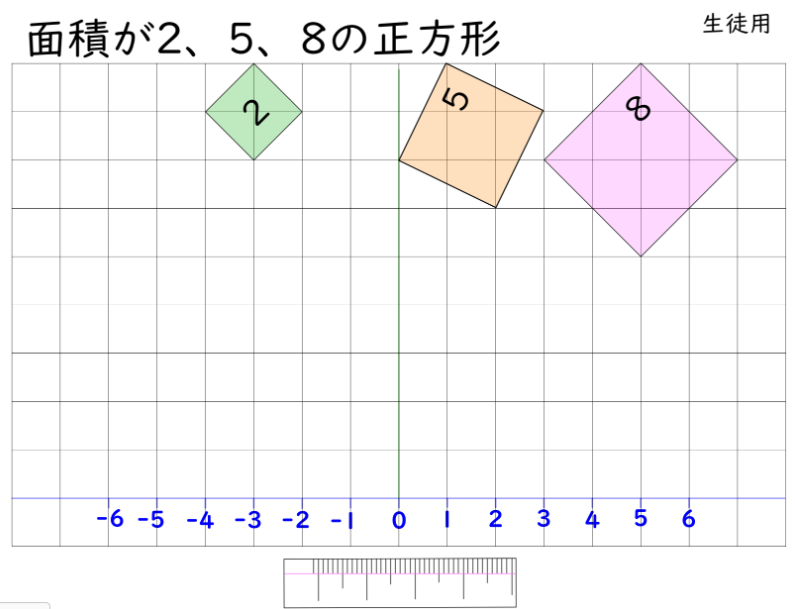
(画像クリックで拡大)
-
作った正方形の左端を、座標軸の原点に移動させて、1辺の長さを確認することが難しいことを理解する
(面積が2,8の正方形は45°回転/面積が5の正方形は約64°回転させて移動) -
物差しのアイテムを数直線下に移動させ、1辺の長さのおおよその値を求めさせる。
※はっきりと数値にあらわせない長さが、数直線上に存在することを認識させる。 - 作った正方形の右端を、座標軸の原点に移動させて、負の数を確認する(-2,-3,-4)
3.無理数の存在を知り、その表現方法を学ぶ
- ここまでの操作活動を通して知った、はっきりと数値に表せない長さの表現方法として、根号を使うことを学習する。
- 根号を使わなくてもよい数字(平方数の平方根)についても学習する。
4.無理数を含め、数の大小を不等号を使って表す
- 操作活動で使った数直線を見ながら、2,3,4,√2,√5,√8の大小関係を不等号を使って表す。
- 同じように、-√2,-√5,-√8の大小関係を不等号を使って表す。
5.まとめ
- 分数(や小数)で表すことのできない無理数の存在をしったことを確認する。また、πも無理数であることを押さえる。
- 数直線上で考えることで、無理数とこれまでの数字の大小関係を表すことができることを確認する。
- 余裕があれば、8の正方形は、面積が2の正方形とくらべ、一辺が2倍の長さであることを押さえ、√8=2√2を教えるときの伏線をはっておきたい。