MetaMoJi ClassRoom先生 授業例
【中3 数学】三平方の定理のパズル（啓林館 ７章 三平方の定理）
熊本県 熊本市立植木北中学校 堀之内聖二先生
■ 単元目標
- 複数のパズルに取り組むことで、直角三角形の３辺の長さの関係に気づく。
- 三平方の定理の証明に意欲的に取り組む。
■ MetaMoJi ClassRoom を導入した利点と成果
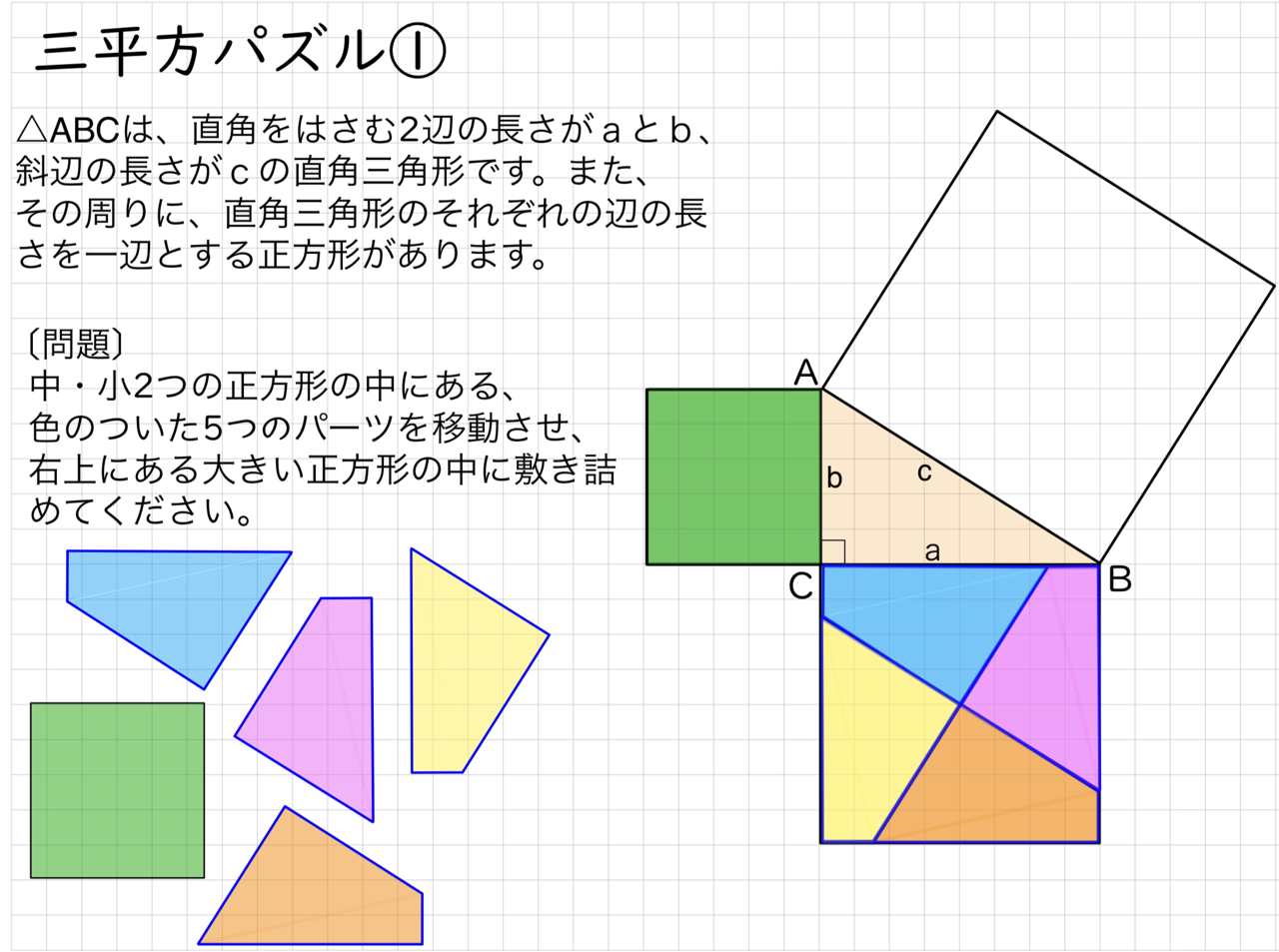
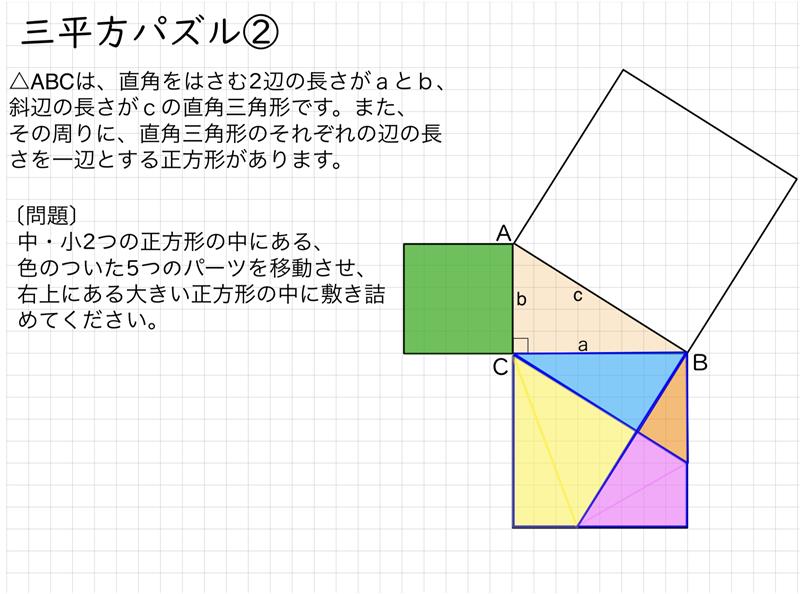
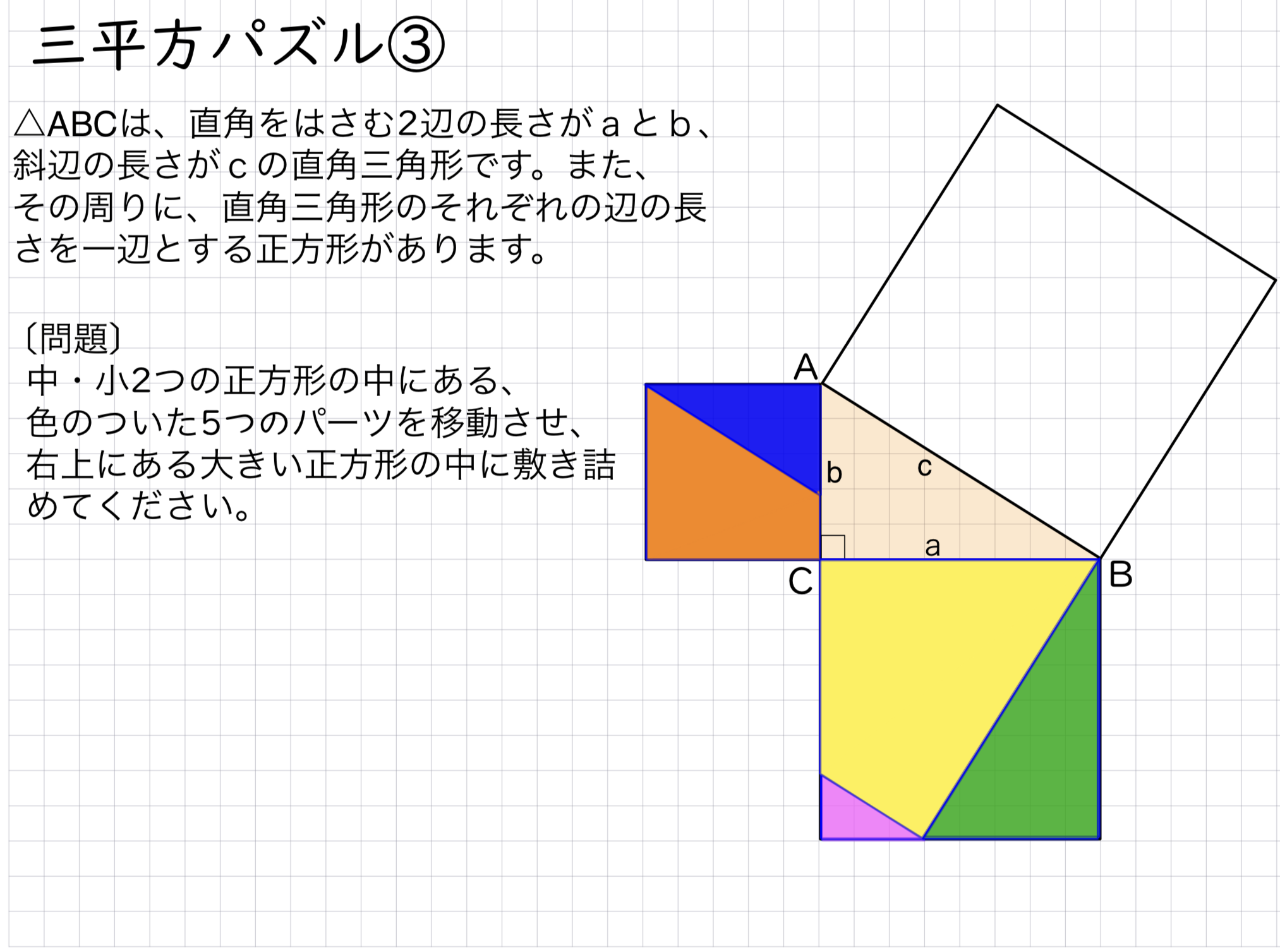
三平方の定理の導入として、昔から紙を切って並び替えるパズルが存在していたが、そのパズルをメタモジの図形機能で作成した。
- 紙を切ったり、糊で貼ったりする時間がなくなり、時間の短縮ができた。
- 作業の進み具合をリアルタイムで確認できるので、作業が遅れている生徒の取りこぼしが生まれなかった。
- iPadを利用することで生徒の興味関心を高めることができた。とても楽しくパズルに取り組んでいた。
- 他のアプリでは学習の記録が残らないが、配布したワークシート内で取り組むので、復習にいつでも活用できる。
■ 学習活動
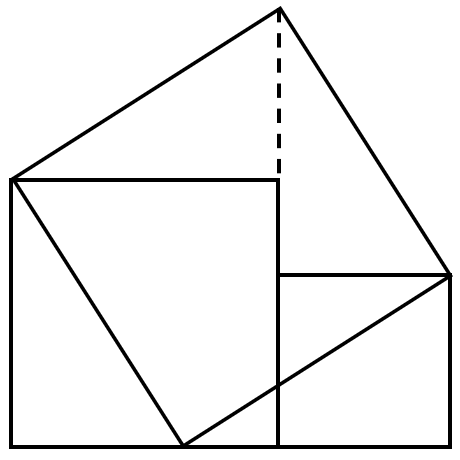
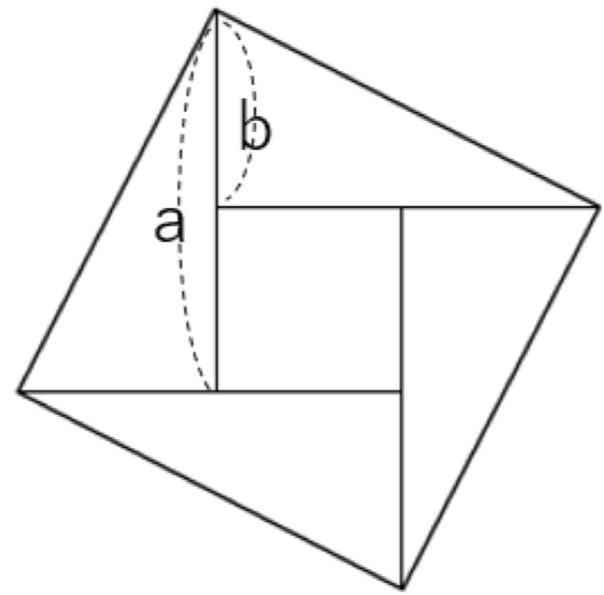
1.三平方のパズルを解く
三平方のパズル①〜③に取り組む。
（画像クリックで拡大）
（画像クリックで拡大）
（画像クリックで拡大）
2.パズルの結果から、直角三角形の３辺の関係を考察する
〔話し合い活動〕
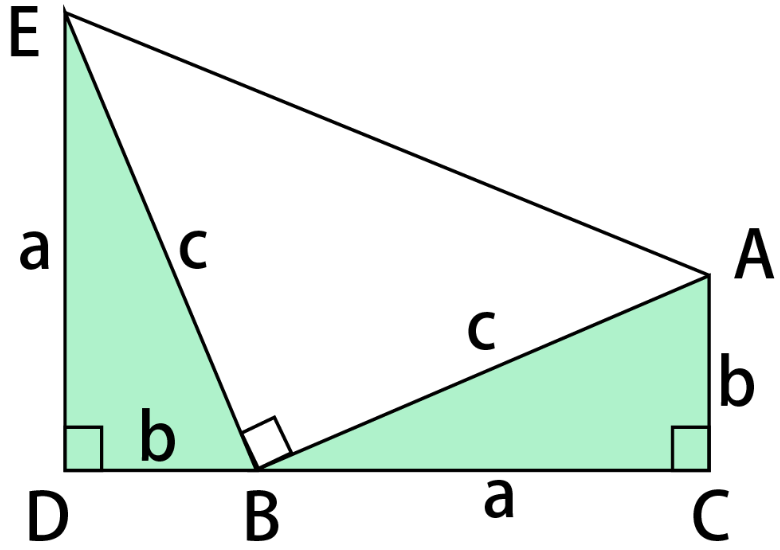
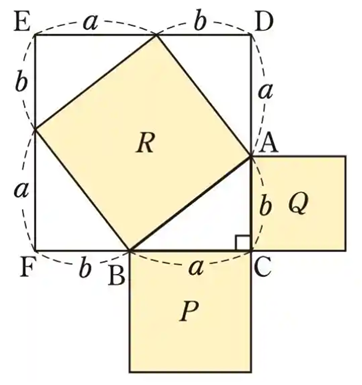
- パズルの結果から、直角三角形の斜辺以外のそれぞれの辺の長さの２乗の和が、斜辺の長さの２乗と等しいことに気づく。
- パズルの切り方から、どんな直角三角形であっても、パズルの結果が成り立つことが理解できる。
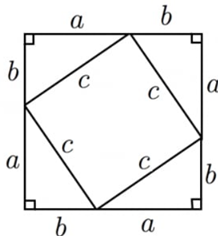
3.三平方の定理の証明に取り組む
〔班学習〕
先生から、三平方の定理／ピタゴラスの定理の説明と、歴史的に多くの証明方法が存在することを聞く。提示されたいくつかの図の中から、班で一つを選び、その図を使って証明できないかに取り組む。
- メタモジ（グループ学習ページ）
（画像クリックで拡大）
（画像クリックで拡大）
（画像クリックで拡大）
（画像クリックで拡大）
（画像クリックで拡大）
4.三平方の定理の証明を発表する
〔一斉学習〕
班ごとに「みんなに見せる」画面にして、自分の班の証明を説明する。
5.まとめ
- 直角三角形は２辺の長さがわかれば、三平方の定理と二次方程式を利用して、残りの１辺の長さが求められることをまとめる。
- 簡単な問題を解いて、三平方の定理の便利さを実感する。
- 三平方の定理の発展性は広く、これからその学習をしていくということを伝える。